АНАЛИТИЧЕСКИЕ ФУНКЦИИ
функции, к-рые могут быть представлены степенными рядами.
Исключительная важность класса А. ф. определяется следующим. Во-первых,
этот класс достаточно широк; он охватывает большинство функций, встречающихся
в основных вопросах математики и её приложений к естествознанию и технике.
Аналитическими являются элементарные функции - многочлены, рациональные
функции, показательная и логарифмическая, степенная, тригонометрические
и обратные тригонометрические, гиперболические и им обратные, алгебраические
функции, и специальные функции - эллиптические, цилиндрические и др.
Во-вторых,
класс А. ф. замкнут относительно основных операций арифметики, алгебры
и анализа; применение арифметич. действий к функциям этого класса, решение
алгебраических ур-ний с аналитич. коэфф., дифференцирование и интегрирование
А. ф. приводят снова к А. ф. Наконец, А. ф. обладают важным свойством единственности;
каждая А. ф. образует одно "органически связанное целое", представляет
собой "единую" функцию во всей своей естественной области существования.
Это свойство, к-рое в 18 в. считалось неотделимым от самого понятия функции,
приобрело принципиальное значение после установления в 1-й пол. 19 в. общей
точки зрения на функцию как на произвольное соответствие.
Теория А. ф.
создана в 19 в., в первую очередь благодаря работам О. Коши, Б. Римана
и К. Вейерштрасса. Решающую роль в построении этой теории сыграл "выход
в комплексную область" - переход от действительного переменного x к комплексному
переменному z == х + iу, к-рое может меняться в произвольной области комплексной
плоскости. Теория А. ф. возникла как теория функций комплексного переменного;
в нек-ром смысле именно аналитические (а не произвольные комплексные функции
двух действительных переменных х и у) естественно считать функциями комплексного
переменного г. Теория А. ф. составляет основное содержание общей теори
ч функций комплексного переменного. Поэтому часто под теорией функций комплексного
переменного понимают именно теорию А. ф.
Существуют
различные подходы к понятию аналитичности. В основе одного из них, впервые
развитого Коши и далеко продвинутого Риманом, лежит структурное свойство
функции - существование производной по комплексному переменному, или комплексная
дифференцируемость. Этот подход тесно связан с геометри ч. соображениями.
Другой подход, систематически развивавшийся Вейер-штрассом, основывается
на возможности представления функций степенными рядами; он связан, тем
самым, с аналитич. аппаратом, к-рым может быть изображена функция. Основной
факт теории А. ф. заключается в тождественности соответствующих классов
функций, рассматриваемых в произвольной области комплексной плоскости.
Приведём точные
определения. Всюду в дальнейшем через z обозначается комплексное число
х + ГУ , где х и у - действительные числа. Геометрически число г изображается
точкой плоскости с координатами х и у; евклидова плоскость, точки к-рой
отождествляются с комплексными числами, наз. комплексной плоскостью. Пусть
D - область (открытое связное множество) в комплексной плоскости. Если
каждой точке z области D приведено в соответствие нек-рое комплексное число
w, то говорят, что в области D определена (однозначная) функция f комплексного
переменного z, и пишут: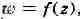
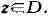
Функция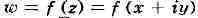 комплексного переменного
комплексного переменного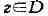 может
может
рассматриваться как комплексная функция двух действительных переменных
х и и, определённая в области D. Полагая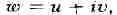
где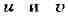 - действительные числа, замечают, что
- действительные числа, замечают, что
задание такой функции f эквивалентно заданию двух действительных функций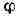
и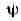 двух действительных переменных х и у, определённых
двух действительных переменных х и у, определённых
в той же области:
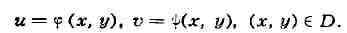
Пусть z - фиксированная
точка области D. Придадим 2 произвольное приращение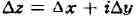
(так, чтобы точка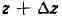 оставалась в пределах области
оставалась в пределах области
О) и рассмотрим соответствующее приращение функции f: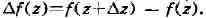
Если разностное отношение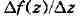 имеет предел при
имеет предел при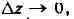
т. е. существует комплексное число А та-
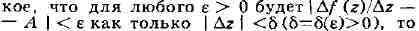
функция f наз.
моногенной в точке г, а число А - её производной в этой точке;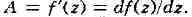
Функция, моно-генная в каждой точке области D, наз. моногенной в области
D.
Если функция
f моногенна в точке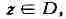 то f и соответствующие функции
то f и соответствующие функции
ф и пси имеют в этой точке частные производные по
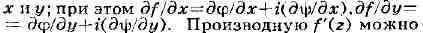
выразить через
частные производные f по х и по у (достаточно вычислить предел отношения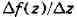
двумя разными способами - при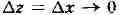 и при
и при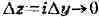 );
);
приравнивая соответствующие выражения, получаем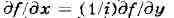
или, что то же самое,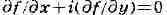 . Переходя к функциям
. Переходя к функциям
и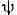 , это равенство можно переписать так:
, это равенство можно переписать так: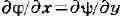
, . Если функция f моногенна в области D,
. Если функция f моногенна в области D,
то последние соотношения справедливы в каждой точке области D; они наз.
уравнениями Коши - Римана. Следует отметить, что эти ур-ния встречались
уже в 18 в. в связи с изучением функций комплексногопере-менного в трудах
Д'Аламбера и Л. Эйлера.
Моногенность
функции f эквивалентна её дифференцируемости в смысле комплексного анализа.
При этом под дифференцируемостью f в точке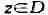 понимается
понимается
возможность представления её приращения в виде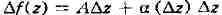
где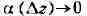
при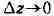 ; дифференциал
; дифференциал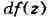
функции f в точке Z, равный главной части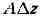
её приращения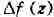 , в этом случае пропорционален
, в этом случае пропорционален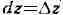
и имеет вид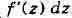 Полезно сравнить понятия дифференцируемости
Полезно сравнить понятия дифференцируемости
функции f - в смысле действительного анализа и в смысле комплексного анализа.
В первом случае дифференциал
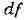
имеет вид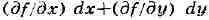 . Удобно переписать это выражение
. Удобно переписать это выражение
в комплексной форме. Для этого переходят от независимых переменных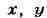
к переменным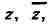 к-рые формально можно считать новыми
к-рые формально можно считать новыми
независимыми переменными, связанными со старыми соотношениями: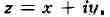
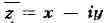
(становясь на эту точку зрения, функцию f иногда записывают в виде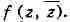
Выражая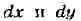 через
через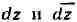
по обычным правилам вычисления дифферен-
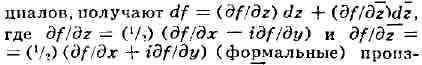
водные функции
f по z и 2 соответственно-Отсюда уже нетрудно заключить, что дифференцируемость
функции f в смысле комплексного анализа имеет место в том и только том
случае, когда она дифференцируема в смысле действительного анализа и справедливо
равенство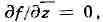 являющееся краткой формой записи
являющееся краткой формой записи
ур-ний Коши - Римана; при этом
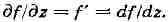
Равенство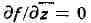
показывает, что дифференцируемыми в смысле комплексного анализа являются
те и только те функции f, к-рые, рассматриваемые формально как функции
независимых переменных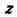 и
и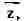
"зависят только от z", являются "функциями комплексного переменного z".
Интеграл от
функции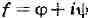 вдоль (ориентированной спрямляемой)
вдоль (ориентированной спрямляемой)
кривой Г можно определить с помощью понятия криволинейного интеграла:
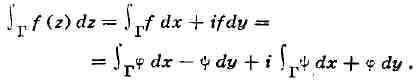
Центральное
место в теории моногенных функций (теории Коши) занимает следующая интегральная
теорема К о-ш и: если функция моногенна в односвязной области D, то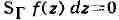
для любой замкнутой кривой Г, лежащей в этой области. В произвольной области
D то же утверждение справедливо для замкнутых кривых Г, к-рые непрерывной
деформацией могут быть стянуты в точку (оставаясь в пределах области D).
Опираясь на интегральную теорему Коши, нетрудно доказать ннте тральную
формулу Кош и: если функция f моногенна в области D и Г - простая замкнутая
кривая, принадлежащая области D вместе со своей внутренностью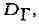
то для любой точки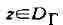
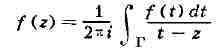
(ориентация
Представим
; поэтому ряд
ряд - после
сходящийся
Уточним теперь
Если это свойство
Выше было показано,
наз. рядом
области D функция
Следовательно,
Важнейшее свойство
Если Е - произвольное
Важную роль
содержащий,
то точка ZD
Функции, представимые
Часто аналитическими
сходящимися
Функции, мероморфные
Для изучения
Дифференцируя
т. е. являются
Всё сказанное
такими функциями
Исходным является
которого является непосредственным
элемент W Совокупность
Полная А. ф.
Фиксируем область ветви функций Понятие А.
Лит.: Привалов
ская теория
А
Б
В
Г
Д
Е
Ё
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Щ
Ъ
Ы
Ь
Э
Ю
Я
кривой Г предполагается положительной относительно области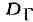
) Пусть функция f моногенна в области D. Фиксируем произвольную точку г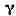 окружность с
окружность с
центром в точке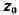 и радиусом
и радиусом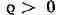 ,
,
принадлежащую, вместе со всем кругом К;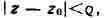 области
области
D. Тогда
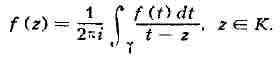
ядро Коши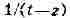 для
для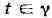
и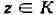 в виде суммы бесконечной геометрич.
в виде суммы бесконечной геометрич.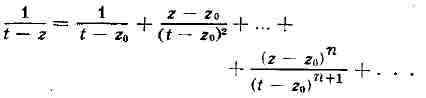
прогрессии:
сходится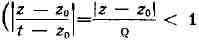 равномерно относительно
равномерно относительно
при любом фиксированном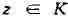 ); интегрируя этот
); интегрируя этот
умножения на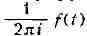 - почленно, получают разложение
- почленно, получают разложение
функции f в степенной ряд
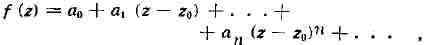
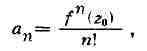
в круге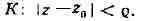
понятие аналитичности. Пусть f - функция, определённая в области D; она
наз. аналитической (или голоморфной) в точке z
f представляется степенным рядом:
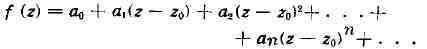
имеет место в каждой точке z
что функция f, моногенная в области D, аналитпчна в этой области. В отдельной
точке это утверждение неверно; напр., функция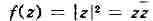 моногенна
моногенна
в точке z
(бесконечно дифференцируема) по комплексному переменному г; коэффициенты
ряда могут быть выражены через производные функции f в точке z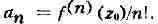 Степенной ряд, записанный в
Степенной ряд, записанный в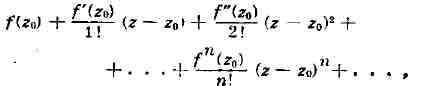
форме
Тейлора функции f в точке z
f бесконечно дифференцируема и её ряд Тейлора сходится к ней в нек-рой
окрестности этой точки.
понятия моногенности и аналитичности функции в области тождественны и каждое
из следующих свойств функции f в области D - моногенность, дифференцируемость
в смысле комплексного анализа, дифференцируемость в смысле действительного
анализа вместе с выполнением ур-ний Коши - Римана - может служить определением
аналитичности f в этой области.
А. ф. выражается следующей теоремой единственности: две функции, аналитические
в области D и совпадающие на каком-либо множестве, имеющем предельную точку
в D, совпадают и во всей области D (тождественны). В частности, аналитическая
в области функция, отличная от тождественного нуля, может иметь в области
лишь изолированные нули.
множество (в комплексной плоскости и, в частности, на действительной прямой),
то функция наз. аналитической на множестве
наз. аналитической на множестве
Е, если каждая точка этого множества имеет окрестность, на пересечении
к-рой с множеством Е функция f представляется сходящимся степенным рядом;
это означает в действительности, что f ана-литична на нек-ром открытом
множестве, содержащем Е (точнее, существует открытое множество, содержащее
Е, и аналитическая на нём функция f, совпадающая с f на множестве Е). Для
открытых множеств понятие аналитичности совпадает с понятием дифференцируемости
по множеству (моногенности). Однако в общем случае это не так; в частности,
на действительной прямой существуют функции, не только имеющие производную,
но и бесконечно дифференцируемые в каждой точке, к-рые не являются аналитическими
ни в одной точке этой прямой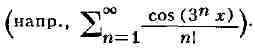 С другой
С другой
стороны, для справедливости теоремы единственности А, ф, существенно свойство
связности множества Е. Поэтому А. ф. рассматриваются обычно в областях,
т. е. на открытых и связных множествах.
в изучении А. ф. играют точки, в к-рых нарушается свойство аналитичности
- т. н. особые точки А. ф. Рассмотрим здесь изолированные особые точки
(однозначных) А. ф. Пусть f - А. ф. в области вида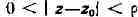
; в этой области f разлагается вряд Лорана:
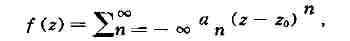
вообще говоря, не только положительные, но и отрицательные степени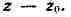
Если в этом разложении члены с отрицательными степенями отсутствуют (a
функцию, аналитическую во всём круге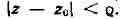 Если ряд Лорана
Если ряд Лорана
функции f содержит лишь конечное число членов с отрицательными степенями
г - Zo'.
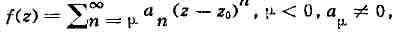
наз. полюсом функции f (порядка д); полюс 2о характеризуется тем, что .
В случае, если ряд Лорана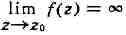 содержит бесконечное
содержит бесконечное
число отрицательных степеней z - z
предела функции f. Если z
f в точке z
в виде отношения двух функций, аналитических в области D, наз. мероморфными
в области D. Мероморфная в области функция аналитична в этой области за
исключением, быть может, конечного или счётного множества полюсов; в полюсах
значения мероморфной функции считаются равными бесконечности. Если допустить
такие значения, то мероморфные в области D функции могут быть определены
как функции, к-рые в окрестности каждой точки 2„ области D представимы
рядом по степеням z - z
в области D наз. как аналитические (голоморфные), так и мероморфные в этой
области функции. В этом случае голоморфные функции наз. также регулярными
аналитическими или просто регулярными. Простейший класс А. ф. составляют
функции, аналитические во всей плоскости; такие функции наз. целыми. Целые
функции представляются рядами вида
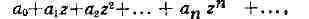
во всей комплексной плоскости. К ним относятся многочлены от z, функции
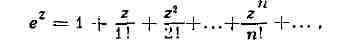
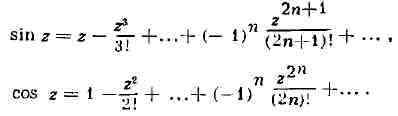
во всей плоскости (т. е. представимые в виде отношения целых функций),
наз. мероморфными функциями. Таковыми являются рациональные функции от
z (отношения многочленов), , , эллиптические функции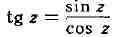
и т. д.
д.
А. ф. важное значение имеют связанные с ними геом. представления. Функцию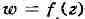
, можно рассматривать как отображение области
можно рассматривать как отображение области
D в плоскость переменного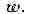 Если f есть А.
Если f есть А.
ф., то образ f(D) области D также является областью (принцип сохранения
облает и). Из условия комплексной дифференцируемости функции f в точке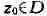
следует, что при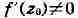 соответствующее отображение
соответствующее отображение
сохраняет углы в z
и важным геом. понятием конформного отображения. Если f аналитична в D
и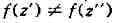 при
при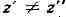 (такие функции
(такие функции
наз. однолистным и), то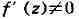 в D н f определяет
в D н f определяет
взаимно однозначное и конформное отображение области D на область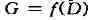
Теорема Римана - основная теорема теории конформных отображений - утверждает,
что в любой односьязной области, граница к-рой содержит более одной точки,
существуют однолистные А. ф., конформно отображающие эту область на круг
или полуплоскость.
ур-ния Коши - Римана, нетрудно усмотреть, что действительная и мнимая части
функции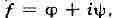 аналитич. в области D, удовлетворяют в
аналитич. в области D, удовлетворяют в
этой области ур-нию Лапласа;
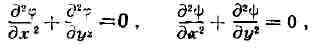
гармоническими функциями. Две гармонич. функции, связанные между собой
ур-ниями Коши - Римана, наз. сопряжёнными. В односвязной области D любая
гармонич. функция ф имеет сопряжённую функцию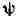
и является, тем самым, действительной частью нек-рой аналитической в D
функции f. Связи с конформными отображениями и гармонич. функциями лежат
в основе многих приложений теории А. ф.
выше относилось кодно-значным А. ф. f, рассматриваемым в данной области
D комплексной плоскости. Задаваясь вопросом о возможности продолжения функции
f как А. ф. в большую область, приходят к понятию А. ф., рассматриваемой
в целом - во всей своей естественной области существования. При таком продолжении
данной функции область её аналитичности, расширяясь, может налегать сама
на себя, доставляя новые значения функции в точках плоскости, где она уже
была определена. Поэтому А. ф., рассматриваемая в целом, вообще говоря,
оказывается многозначной. К необходимости изучения многозначных А. ф. приводят
многие вопросы теории функций (обращение функций, нахождение первообразных
и построение А. ф. с заданной действительной частью - в многосвязных областях,
решение алгебр, ур-ний с аналитич. коэфф. и др.);
являются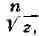
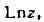 Arcsin г и Arctg
Arcsin г и Arctg
z, алгебр, функции и т. д. Регулярный процесс, приводящий к полной А. ф.,
рассматриваемой в своей естественной области существования, был указан
К. Вейерштрассом; он носит название аналитического продолжения по Вейерштрассу.
понятие элемента А. ф.- степенного ряда с ненулевым радиусом сходимости.
Такой элемент W
круге сходимости К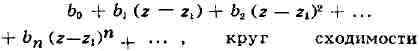
обозначают через /С,. В общей части кругов K
аналитич. продолжением тогда
тогда
значениям функции в круге К
всех элементов, к-рые могут быть получены аналитич. продолжением элемента
Wo. образует полную А. ф. (в смысле Вейерштрасса), порождённую элементом
W
что А. ф, в смысле Вейерштрасса полностью определяется заданием элемента
Wo- При этом в качестве исходного может быть взят любой др. элемент, принадлежащий
этой функции; полная А. ф. от этого не изменится.
f, рассматриваемая как функция точек плоскости, принадлежащих её области
существования D, вообще говоря, является многозначной. Чтобы избавиться
от многозначности, функцию f рассматривают не как функцию точек плоской
области D, а как функцию точек нек-рой (лежащей над областью D)) многолистной
поверхности R такой, что каждой точке области D соответствует столько (проектирующихся
в неё) точек поверхности R, сколько различных значений принимает функция
f в этой точке; на поверхности R функция f становится однозначной функцией.
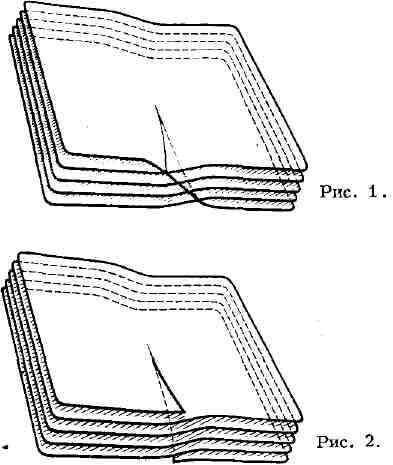
Идея перехода к таким поверхностям - одна из наиболее замечательных и плодотворных
математич. идей - принадлежит Б. Рима-ну, а сами они носят назв. римановых
поверхностей. Схематич. изображения римановых поверхностей функций
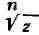
и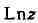 приведены на рис. 1 и 2 (соответственно).
приведены на рис. 1 и 2 (соответственно).
Абстрактное определение понятия римановой поверхности позволило заменить
теорию многозначных А. ф. теорией однозначных А. ф. на риманоаых поверхностях.
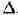 ,
,
принадлежащую области существования D полной А. ф. f, и какой-либо элемент
W функции f с центром в точке области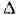 . Совокупность
. Совокупность
всех элементов, к-рые могут быть получены ана-литич. продолжением элемента
W посредством цепочек, центры к-рых принадлежат Д, наз. ветвью А. ф. f.
Ветвь многозначной А. ф. может оказаться однозначной А. ф. в области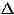 .
.
Так, напр., произвольные
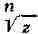
и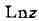 , соответствующие любой односвязной области,
, соответствующие любой односвязной области,
не содержащей точку О, являются однозначными функциями; при этом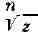 имеет
имеет
ровно п, a Lnz - бесконечное множество различных ветвей в каждой такой
области. Выделение однозначных ветвей (с помощью тех или иных разрезов
области существования) и их изучение средствами теории однозначных А. ф.
являются одним из основных приёмов исследования конкретных многозначных
А. ф.
ф. нескольких переменных вводится с помощью кратных степенных рядов - совершенно
аналогично тому, как это было сделано выше для А. ф. одного переменного.
А. ф. нескольких комплексных переменных по своим свойствам также во многом
аналогичны А. ф. одного комплексного переменного; однако они обладают и
рядом принципиально новых свойств, не имеющих аналогов в теории А. ф. одного
переменного. Более общим является понятие А. ф. на комплексных многообразиях
(понятие комплексного многообразия является обобщением понятия римановой
поверхности для многомерного случая).
И, И., Введение в теорию функций комплексного переменного, 11 изд., М.,
1967; Смирнов В. И., Курс высшей математики, 8 изд., т. 3, ч. 2, М.- Л.,
1969; Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1-2, М.,
1967-68; Лаврентьев М.А., Шабат Б. В., Методы теории функций комплексного
переменного, 3 изд., М., 1965; Голузин Г. М., Геометриче-
функций комплексного переменного, 2 изд., М., 1966; Евграфов М. А., Аналитические
функции, 2 изд., М., 1968; Свешников А. Г., Тихонов А. Н., Теория функций
комплексной переменной, М., 1967; Фукс Б. А., Теория аналитических функций
многих комплексных переменных, 2 изд., М., 1963; Владимиров В. С., Методы
теории функций многих комплексных переменных, М., 1964; Маркушевич А. И.,
Очерки по истории теории аналитических функций, М.- Л., 1951; Математика
в СССР за тридцать лет, 1917 - 1947, М.- Л., 1948, с. 319 - 414; Математика
в СССР за сорок лет, 1917 - 1957, т. 1, М., 1959, с. 381 - 510. А. А. Гончар.